Sztuczne sieci neuronowe w Matlabie – zrozum net.IW, LW i bMay 2009

W ramach projektu ze Sztucznej Inteligencji mieliśmy stworzyć sieć neuronową, która będzie odpowiadała, czy punkt S = [x, y] należy do kwadratu spełniającego układ nierówności:

• x > 2
• x < 6
• y > 3
• y < 7

Sieć neuronowa powinna być utworzona na dwa sposoby.

1. Poprzez nauczenie sieci neuronowej przykładowymi danymi.
2. Poprzez ręczne ustawienie wag oraz współczynników poszczególnym neuronom.

Wykonanie punktu pierwszego nie jest zbyt trudne, ponieważ w sieci dostępnych jest bardzo dużo przykładów. Kłopoty rozpoczynają się przy drugim zadaniu. Dokumentacja Neural Toolbox w Matlabie co prawda jest bardzo dobra, ale akurat kwestię ręcznego przypisywania wag opisuje słabo. Stąd też tylko metodą prób i błędów można próbować zrozumieć sposób tworzenia sztucznych sieci neuronowych w Matlabie. Dwa dni prób mam za sobą i teraz mogę się podzielić swoją wiedzą.

Najpierw należy rozpocząć od analizy problemu. Mamy zwrócić wartość 1 dla punktów, które spełniają pewien układ nierówności. Każdy jeden neuron w sieci neuronowej potrafi zrealizować jedną prostą oddzielającą klasy. W związku z tym w warstwie ukrytej sieci neuronowej potrzebujemy czterech neuronów. Wejścia są dwa - x oraz y, a wyjście jest jedno i zwraca wartość 0 lub 1. Szkic pożądanej sieci neuronowej przedstawia się następująco:

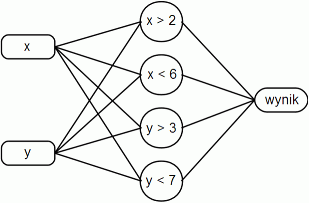
net = newff([-10 10; -10 10], [4 1], {'hardlim', 'hardlim'});
% pierwszy parametr - zakresy kolejnych wejść
% drugi parametr - ilość neuronów w każdej kolejnej warstwie
% trzeci parametr - funkcje przynależności, np. hardlim, tansig, logsig, purelin, satlin

% Obejrzyj na wykresie, jak się zachowują poszczególne funkcje przynależności:
% plot(-10: 0.1 : 10, tansig(-10: 0.1 : 10))

Jak widać, każdy neuron realizuje pewną funkcję. Żeby jednak pierwsze dwa neurony działały poprawnie, należy na ich wejście doprowadzić tylko wartość x. W tym celu ustawiamy wagę wejścia y na 0 dla tych neuronów. Analogicznie czynimy dla neuronów trzeciego i czwartego, ustawiając wagi dla wejść x na 0. Takim zabiegiem sieć neuronowa działa, jak gdyby nie było połączeń pomiędzy wejściem x i dolnymi neuronami oraz wejściem y i górnymi neuronami.

% Tak mniej więcej powinny wyglądać wagi.
% Jedynki mogą się zmienić później, jednak zera zostaną.

% Waga X dla kolejnych neuronów
net.IW{1}(:,1) = [1; 1; 0; 0];
% Waga Y dla kolejnych neuronów
net.IW{2}(:,2) = [0; 0; 1; 1];

Teraz przyjrzymy się pierwszemu neuronowi, mającemu realizować zadanie x > 2. Każdy neuron realizuje pewną matematyczną funkcję. W tym przykładzie funkcję hardlim. Wartość na wyjściu neurona liczona jest wg wzoru: a = hardlim(w * x + b). Zatem, aby funkcja zwracała wartość 1 dla x > 2, współczynnik wagowy w powinien wynosić 1, zaś b -2.

net.IW{1}(1,1) = 1;
net.b{1}(1) = -2;

% Skorzystaj z polecenia nnd2n1, aby wspomóc sobie dobieranie wag graficznie.

Prostą x < 6 zrealizujemy w podobny sposób. Trzeba tylko zmienić stronę - funkcja hardlim ma zwracać wartość 1 nie na prawo, lecz na lewo od szóstki. W tym celu wagę ustawimy na -1, a współczynnik b na 6. Podobne działania wykonujemy dla neuronów dolnych.

Teraz każdy neuron realizuje swoją pożądaną funkcję. Przejdźmy więc do neurona wyjściowego. Neuron wyjściowy powinien zwracać 1 wtedy i tylko wtedy, gdy każdy z neuronów poprzedzających zwrócił wartość 1. Należy wiedzieć, że jeśli do dowolnego neurona podłączone są dwa wejścia i na jednym wejściu wchodzi wartość 2, a na drugim 3, to neuron otrzymuje sumę tych wartości, czyli 5. Z tego wynika, że neuron końcowy powinien zwracać wartość 1 tylko, jeśli na wejściu otrzymał sumę równą 4. W tym celu wagi wszystkich wejść ustawiamy na 1, a współczynnik b na -4.

% Kompletny kod:

% Utworzenie sieci neuronowej o dwóch wejściach i jednym wyjściu
net = newff([-10 10; -10 10], [4 1], {'hardlim', 'hardlim'});

% Ustalenie współczynników b
net.b{1} = [-2; 6; -3; 7];

% Wejście X - wagi wejściowe dla kolejnych neuronów
net.IW{1}(:,1) = [1; -1; 0; 0];
% Wejście Y - wagi wejściowe dla kolejnych neuronów
net.IW{1}(:,2) = [0; 0; 1; -1];

% Ustawienie wag dla neuronów
net.LW{2,1}(1,:) = [1 1 1 1];
net.b{2} = -4;

Zwracam uwagę na nieszczęsne IW oraz LW. net.IW to wagi wejściowe dla pierwszej warstwy neuronów, zaś net.LW to wagi wyjściowe z pierwszej warstwy neuronów.

Wygenerujmy teraz jakieś losowe punkty i sprawdźmy, czy nasza sieć neuronowa działa.

% Wygenerowanie punktów
x1 = rand(1, 80) * 8;
x2 = rand(1, 80) * 8;
obrazy = [x1; x2];
klasy = (obrazy(1,:) > 2) .* (obrazy(1,:) < 6) .* (obrazy(2,:) > 3) .* (obrazy(2,:) < 7 );
ind1 = find(klasy == 0);
ind2 = find(klasy == 1);

% Utworzenie sieci neuronowej o dwóch wejściach i jednym wyjściu
net = newff([-10 10; -10 10], [4 1], {'hardlim', 'hardlim'});

% Ustalenie współczynników b
net.b{1} = [-2; 6; -3; 7];

% Wejście X - wagi wejściowe dla kolejnych neuronów
net.IW{1}(:,1) = [1; -1; 0; 0];
% Wejście Y - wagi wejściowe dla kolejnych neuronów
net.IW{1}(:,2) = [0; 0; 1; -1];

% Ustawienie wag dla neuronów
net.LW{2,1}(1,:) = [1 1 1 1];
net.b{2} = -4;

% Narysowanie wykresu
[X,Y] = meshgrid(0 : 0.1 : 8);
Z = X;
Z(:) = sim(net, [X(:) Y(:)]');
contour(X,Y,Z,[0.499 0.5 0.501]);
hold on
plot(x1(ind1),x2(ind1),'bo',x1(ind2),x2(ind2),'rs')
hold off

Mam nadzieję, że mój artykuł pomógł zrozumieć, w jaki sposób tworzyć sztuczne sieci neuronowe przy pomocy Matlaba. Kluczowym do zrozumienia zagadnienia jest opanowanie właściwości net.IW, net.LW oraz net.b, które są bardzo nieintuicyjne i słabo udokumentowane.